1. Задание № 112 

Сложность: III
Классификатор алгебры: 3\.13\. Системы уравнений
Методы алгебры: Выделение полного квадрата
Системы рациональных уравнений
i
Пусть (x;y) — целочисленное решение системы уравнений
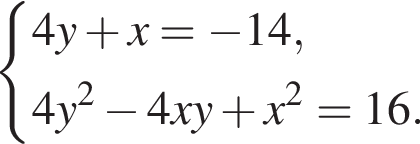
Найдите сумму x+y.
Решение. Выразим x из первого уравнения системы: 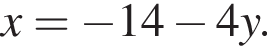 Заметим, что
Заметим, что 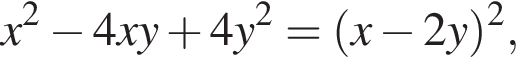 поэтому, подставляя x во второе уравнение системы получим:
поэтому, подставляя x во второе уравнение системы получим:
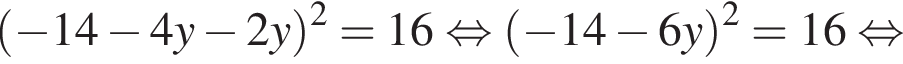
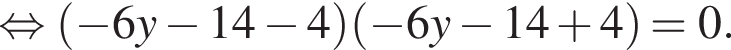
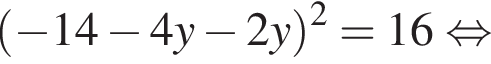
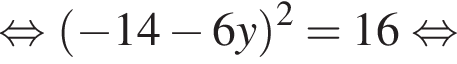
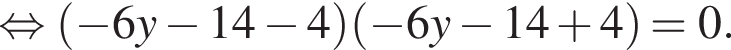
Таким образом, получаем: 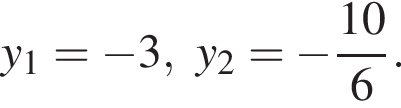 Поскольку по условию задачи требуются целочисленные решения системы, тогда найдем x:
Поскольку по условию задачи требуются целочисленные решения системы, тогда найдем x: 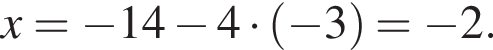 Сумма x+y равна:
Сумма x+y равна: 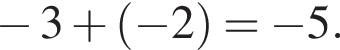
Ответ: −5.
Ответ: -5
112
-5
Сложность: III
Классификатор алгебры: 3\.13\. Системы уравнений
Методы алгебры: Выделение полного квадрата
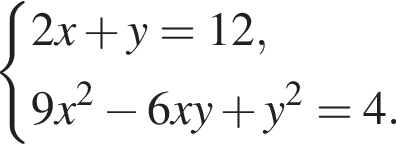
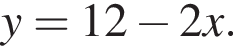 Заметим, что
Заметим, что 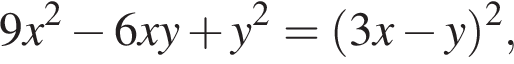 поэтому, подставляя y во второе уравнение системы получим:
поэтому, подставляя y во второе уравнение системы получим: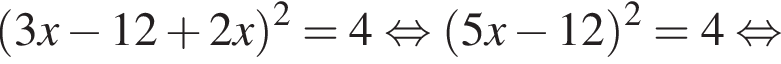
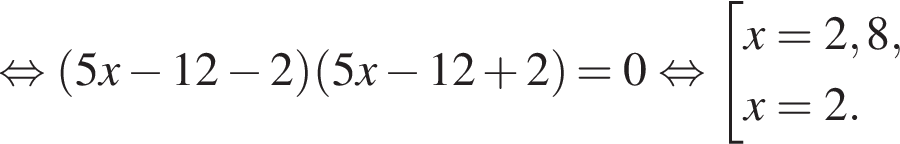
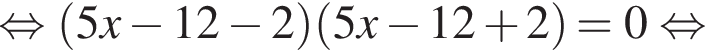
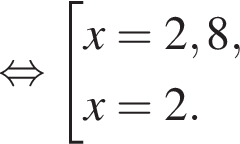
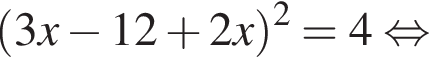
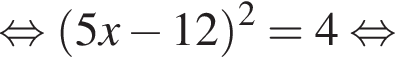
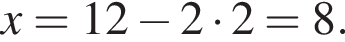 Сумма x+y равна:
Сумма x+y равна: 
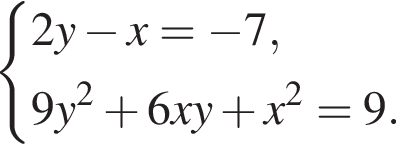
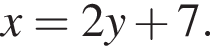 Заметим, что
Заметим, что 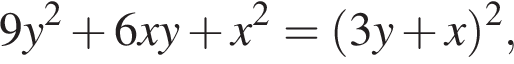 поэтому, подставляя x во второе уравнение системы получим:
поэтому, подставляя x во второе уравнение системы получим:
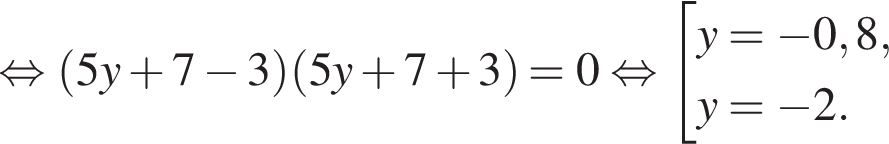
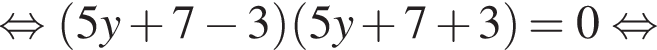
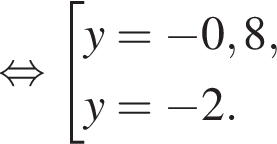
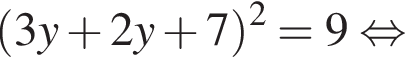
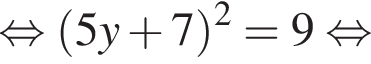
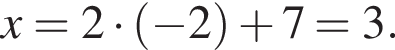 Сумма x+y равна:
Сумма x+y равна: 
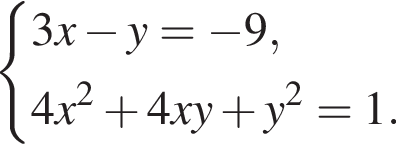
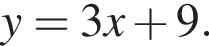 Заметим, что
Заметим, что 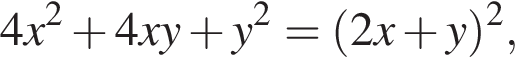 поэтому, подставляя y во второе уравнение системы получим:
поэтому, подставляя y во второе уравнение системы получим:
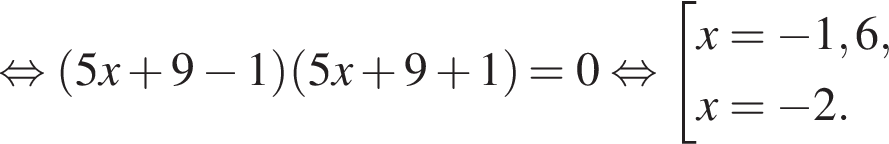
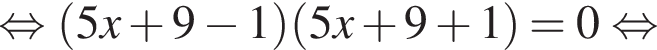
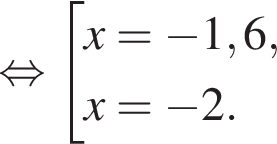
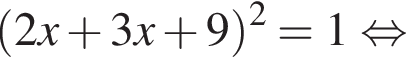
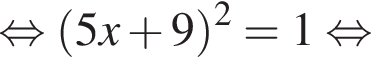
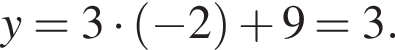 Сумма x+y равна:
Сумма x+y равна: 
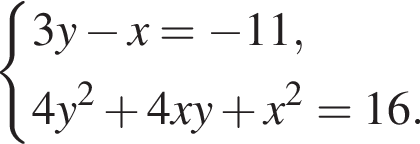
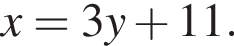 Заметим, что
Заметим, что  поэтому, подставляя x во второе уравнение системы получим:
поэтому, подставляя x во второе уравнение системы получим:
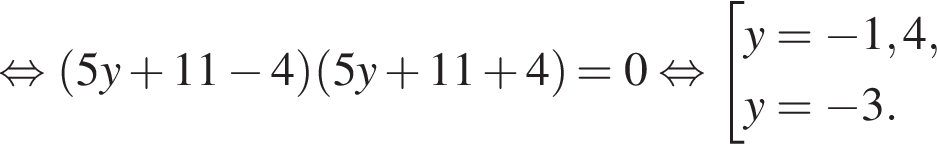

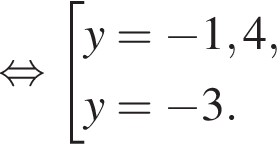
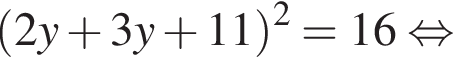
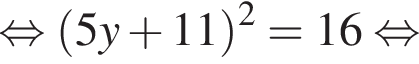
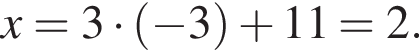 Сумма x+y равна:
Сумма x+y равна: 